평균(mean, average)
어떤 집단을 대표하는 값 중의 하나로, 모든 원소의 값을 다 더한 후 원소의 개수로 나누어주는 값으로 정의됩니다.
분산(Variance)
분산도 평균의 일종으로, 편차를 제곱한 후 이들을 모두 더한 뒤 원소의 개수로 나누어주는 값으로 정의됩니다.
즉, "편차의 제곱의 평균"이 된다. 편차는 "원소의 값 - 평균"으로 각각의 원소값이 평균으로부터 얼마나 떨어져 있는지를 나타냅니다.
표준편차(Standard deviation)
표준편차는 분산을 제곱근한 값이 됩니다. 편차를 모두 더하면 0이 되기 때문에, 분산은 제곱을 한 후 평균을 구하게 됩니다. 제곱을 했으니, 다시 원래 스케일로 돌리기 위해서 제곱근을 해주게 됩니다.
예제
어떤 두 그룹 A,B가 있고, 각각 10명의 키를 조사하였습니다. 해당 내용에 대해 위에 설명한 통계값들을 직접 구해서 살펴봅니다.
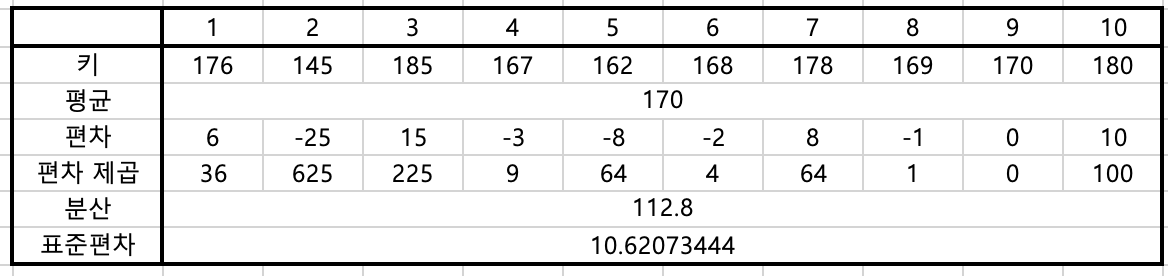
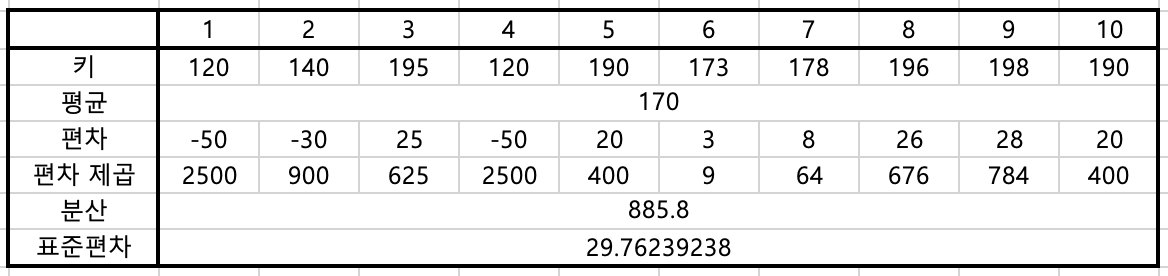
우선, 두 그룹의 평균을 살펴보겠습니다. 모두 170으로 동일합니다. 평균값만으로는 두 그룹의 키가 어떤 분포로 이루어져 있는지 알 수가 없습니다. 다음, 분산을 보겠습니다. A그룹은 112 정도이고, B그룹은 885입니다. B그룹이 훨씬 더 큰 값을 갖는 것을 알 수 있습니다. 이 값의 제곱근이 표준편차이므로 해당 값을 살펴보면 10과 29로 역시 많이 차이가 납니다.
이 값으로 볼 때, A그룹은 대체적으로 키가 170에 가깝게 모여있는 것을 알 수가 있고, B그룹은 평균과 값이 들쑥날쑥하게 멀리 떨어져 있다는 것을 알 수 있습니다. 그래프를 통해서 확인해보겠습니다.
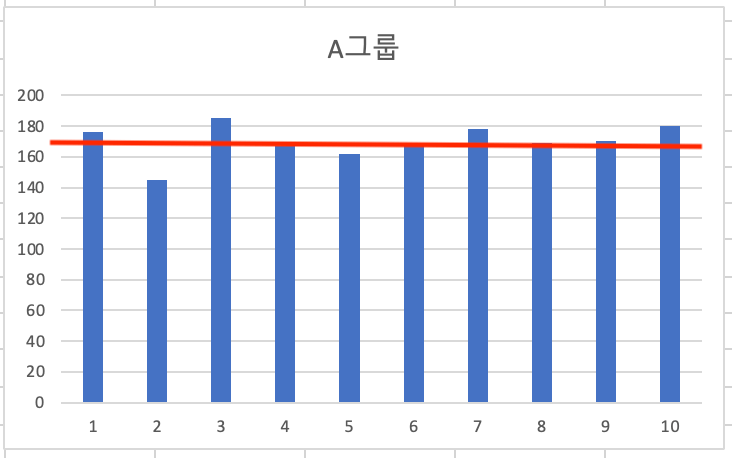
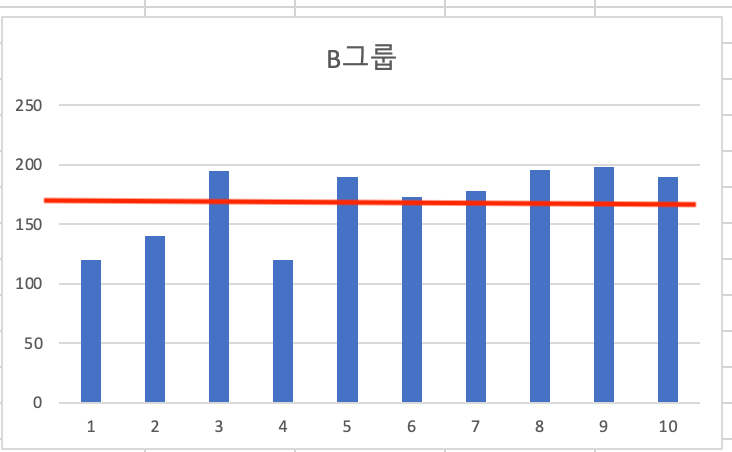
빨간색이 170으로, 평균을 표시해 보았습니다. A그룹은 실제로 키가 평균에 모여있는 것을 볼 수 있고 그 차이는 대략 표준편차값인 10cm 근방이라는 것을 알 수 있습니다.
B그룹의 경우, 대체적으로 30cm 정도 까지도 들쑥날쑥하다는 것을 알 수 있습니다.